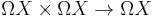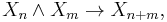Highly structured ring spectrum
In mathematics, a highly structured ring spectrum or  -ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an
-ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an  -ring is called an
-ring is called an 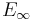 -ring. While originally motivated by questions of geometric topology and bundle theory, they are today most often used in stable homotopy theory.
-ring. While originally motivated by questions of geometric topology and bundle theory, they are today most often used in stable homotopy theory.
Contents |
Background
Highly structured ring spectra have better formal properties than multiplicative cohomology theories - a point utilized, for example, in the construction of topological modular forms, and which has allowed also new constructions of more classical objects such as Morava K-theory. Beside their formal properties, 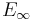 -structures are also important in calculations, since they allow for operations in the underlying cohomology theory, analogous to (and generalizing) the well-known Steenrod operations in ordinary cohomology. As not every cohomology theory allows such operations, not every multiplicative structure may be refined to an
-structures are also important in calculations, since they allow for operations in the underlying cohomology theory, analogous to (and generalizing) the well-known Steenrod operations in ordinary cohomology. As not every cohomology theory allows such operations, not every multiplicative structure may be refined to an 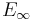 -structure and even in cases where this is possible, it may be a formidable task to prove that.
-structure and even in cases where this is possible, it may be a formidable task to prove that.
The rough idea of highly structured ring spectra is the following: If multiplication in a cohomology theory (analogous to the multiplication in singular cohomology, inducing the cup product) fulfills associativity (and commutativity) only up to homotopy, this is too lax for many constructions (e.g. for limits and colimits in the sense of category theory). On the other hand, requiring strict associativity (or commutativity) in a naive way is too restrictive for many of the wanted examples. A basic idea is that the relations need only hold up to homotopy, but these homotopies should fulfill again some homotopy relations, whose homotopies again fulfill some further homotopy conditions; and so on. The classical approach organizes this structure via operads, while the recent approach of Jacob Lurie deals with it in the language of 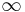 -categories. The most widely used approaches today employ the language of model categories.
-categories. The most widely used approaches today employ the language of model categories.
All these approaches depend on building carefully an underlying category of Spectra.
Approaches for the definition
Operads
The theory of operads is motivated by the study of loop spaces. A loop space ΩX has a multiplication
by composition of loops. Here the two loops are sped up by a factor of 2 and the first takes the interval [0,1/2] and the second [1/2,1]. This product is not associative since the scalings are not compatible, but it is associative up to homotopy and the homotopies are coherent up to higher homotopies and so on. This situation can be made precise by saying that ΩX is an algebra over the little interval operad. This is an example of an 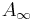 -operad, i.e. an operad of topological spaces which is homotopy equivalent to the associative operad. An
-operad, i.e. an operad of topological spaces which is homotopy equivalent to the associative operad. An 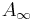 -ring spectrum can now be imagined as an algebra over an
-ring spectrum can now be imagined as an algebra over an 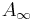 -operad in a suitable category of spectra and suitable compatibility conditions (see May, 1977).
-operad in a suitable category of spectra and suitable compatibility conditions (see May, 1977).
For the definition of 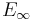 -ring spectra essentially the same approach works, where one replaces the
-ring spectra essentially the same approach works, where one replaces the 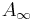 -operad by an
-operad by an 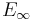 -operad, i.e. an operad of contractible topological spaces. An example of such an operad can be again motivated by the study of loop spaces. The product of the double loop space
-operad, i.e. an operad of contractible topological spaces. An example of such an operad can be again motivated by the study of loop spaces. The product of the double loop space 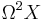 is already commutative up to homotopy, but this homotopy fulfills no higher conditions. To get full coherence of higher homotopies one has to pass to the infinite loop space
is already commutative up to homotopy, but this homotopy fulfills no higher conditions. To get full coherence of higher homotopies one has to pass to the infinite loop space 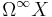 . This leads to the in
. This leads to the in 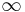 -cube operad of infinite-dimensional cubes in infinite-dimensional space, which is an example of an
-cube operad of infinite-dimensional cubes in infinite-dimensional space, which is an example of an 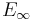 -operad.
-operad.
The above approach was pioneered by J. Peter May. Together with Elmendorf, Kriz and Mandell he developed in the 90s a variant of his older definition of spectra, so called S-modules (see Elmendorf et al, 2007). S-modules possess a model structure, whose homotopy category is the stable homotopy category. In S-modules the category of modules over an 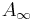 -operad and the category of monoids are Quillen equivalent and likewise the category of modules over an
-operad and the category of monoids are Quillen equivalent and likewise the category of modules over an 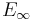 -operad and the category of commutative monoids. Therefore is it possible to define
-operad and the category of commutative monoids. Therefore is it possible to define 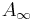 -ring spectra and
-ring spectra and 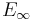 -ring spectra as (commutative) monoids in the category of S-modules, so called (commutative) S-algebras. Since (commutative) monoids are easier to deal with than algebras over complicated operads, this new approach is for many purposes more convenient. It should, however, be noted that the actual construction of the category of S-modules is technically quite complicated.
-ring spectra as (commutative) monoids in the category of S-modules, so called (commutative) S-algebras. Since (commutative) monoids are easier to deal with than algebras over complicated operads, this new approach is for many purposes more convenient. It should, however, be noted that the actual construction of the category of S-modules is technically quite complicated.
Diagram spectra
Another approach to the goal of seeing highly structured ring spectra as monoids in a suitable category of spectra are categories of diagram spectra. Probably the most famous one of these is the category of symmetric spectra, pioneered by Jeff Smith. Its basic idea is the following:
In the most naive sense, a spectrum is a sequence of (pointed) spaces 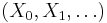 together with maps
together with maps 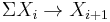 , where ΣX denotes the suspension. Another viewpoint is the following: one considers the category of sequences of spaces together with the monoidal structure given by a smash product. Then the sphere sequence
, where ΣX denotes the suspension. Another viewpoint is the following: one considers the category of sequences of spaces together with the monoidal structure given by a smash product. Then the sphere sequence 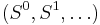 has the structure of a monoid and spectra are just modules over this monoid. If this monoid was commutative, then a monoidal structure on the category of modules over it would arise (as in algebra the modules over a commutative ring have a tensor product). But the monoid structure of the sphere sequence is not commutative due to different orderings of the coordinates.
has the structure of a monoid and spectra are just modules over this monoid. If this monoid was commutative, then a monoidal structure on the category of modules over it would arise (as in algebra the modules over a commutative ring have a tensor product). But the monoid structure of the sphere sequence is not commutative due to different orderings of the coordinates.
The idea is now that one can build the coordinate changes into the definition of a sequence: a symmetric sequence is a sequence of spaces 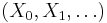 together with an action of the n-th symmetric group on
together with an action of the n-th symmetric group on 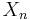 . If one equips this with a suitable monoidal product, one gets that the sphere sequence is a commutative monoid. Now symmetric spectra are modules over the sphere sequence, i.e. a sequence of spaces
. If one equips this with a suitable monoidal product, one gets that the sphere sequence is a commutative monoid. Now symmetric spectra are modules over the sphere sequence, i.e. a sequence of spaces 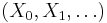 together with an action of the n-th symmetric group on
together with an action of the n-th symmetric group on 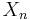 and maps
and maps 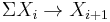 satisfying suitable equivariance conditions. The category of symmetric spectra has a monoidal product denoted by
satisfying suitable equivariance conditions. The category of symmetric spectra has a monoidal product denoted by 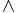 . A highly structured (commutative) ring spectrum is now defined to be a (commutative) monoid in symmetric spectra, called a (commutative) symmetric ring spectrum. This boils down to giving maps
. A highly structured (commutative) ring spectrum is now defined to be a (commutative) monoid in symmetric spectra, called a (commutative) symmetric ring spectrum. This boils down to giving maps
which satisfy suitable equivariance, unitality and associativity (and commutativity) conditions (see Schwede 2007).
There are several model structures on symmetric spectra, which have as homotopy the stable homotopy category. Also here it is true that the category of modules over an 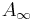 -operad and the category of monoids are Quillen equivalent and likewise the category of modules over an
-operad and the category of monoids are Quillen equivalent and likewise the category of modules over an 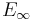 -operad and the category of commutative monoids.
-operad and the category of commutative monoids.
A variant of symmetric spectra are orthogonal spectra, where one substitutes the symmetric group by the orthogonal group (see Mandell et al, 2001). They have the advantage that the naively defined homotopy groups coincide with those in the stable homotopy category, which is not the case for symmetric spectra. On the other hand, symmetric spectra have the advantage that they can also be defined for simplicial sets. Symmetric and orthogonal spectra are arguably the simplest ways to construct a sensible symmetric monoidal category of spectra.
Infinity-categories
Infinity-categories are a variant of classical categories where composition of morphisms is not uniquely defined, but only up to contractible choice. In general, it does not make sense to say that a diagram commutes strictly in an infinity-category, but only that it commutes up to coherent homotopy. One can define an infinity-category of spectra (as done by Lurie). One can also define infinity-versions of (commutative) monoids and then define 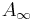 -ring spectra as monoids in spectra and
-ring spectra as monoids in spectra and 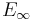 -ring spectra as commutative monoids in spectra. This is worked out in Lurie's book Higher Algebra.
-ring spectra as commutative monoids in spectra. This is worked out in Lurie's book Higher Algebra.
Comparison
The categories of S-modules, symmetric and orthogonal spectra and their categories of (commutative) monoids admit comparisons via Quillen equivalences due to work of several mathematicians (including Schwede). In spite of this the model category of S-modules and the model category of symmetric spectra have quite different behaviour: in S-modules every object is fibrant (which is not true in symmetric spectra), while in symmetric spectra the sphere spectrum is cofibrant (which is not true in S-modules). By a theorem of Lewis, it is not possible to construct one category of spectra, which has all desired properties. A comparison of the infinity category approach to spectra with the more classical model category approach of symmetric spectra can be found in Lurie's Higher Algebra 4.4.4.9.
Examples
It is easiest to write down concrete examples of 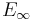 -ring spectra in symmetric/orthogonal spectra. The most fundamental example is the sphere spectrum with the (canonical) multiplication map
-ring spectra in symmetric/orthogonal spectra. The most fundamental example is the sphere spectrum with the (canonical) multiplication map 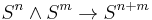 . It is also not hard to write down multiplication maps for Eilenberg-MacLane spectra (representing ordinary cohomology) and certain Thom spectra (representing bordism theories). Topological (real or complex) K-theory is also an example, but harder to obtain: in symmetric spectra one uses a C*-algebra interpretation of K-theory, in the operad approach one uses a machine of multiplicative infinite loop space theory.
. It is also not hard to write down multiplication maps for Eilenberg-MacLane spectra (representing ordinary cohomology) and certain Thom spectra (representing bordism theories). Topological (real or complex) K-theory is also an example, but harder to obtain: in symmetric spectra one uses a C*-algebra interpretation of K-theory, in the operad approach one uses a machine of multiplicative infinite loop space theory.
A more recent approach for finding 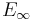 -refinements of mutliplicative cohomology theories is Goerss-Hopkins obstruction theory. It succeeded in finding
-refinements of mutliplicative cohomology theories is Goerss-Hopkins obstruction theory. It succeeded in finding 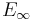 -ring structures on Lubin-Tate spectra and on elliptic spectra. By a similar (but older) method, it could also be shown that Morava K-theory and also other variants of Brown-Peterson cohomology possess an
-ring structures on Lubin-Tate spectra and on elliptic spectra. By a similar (but older) method, it could also be shown that Morava K-theory and also other variants of Brown-Peterson cohomology possess an 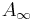 -ring structure (see e.g. Baker and Jeanneret, 2002). Recently, Basterra and Mandell have shown that Brown–Peterson cohomology has even an
-ring structure (see e.g. Baker and Jeanneret, 2002). Recently, Basterra and Mandell have shown that Brown–Peterson cohomology has even an 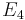 -ring structure, where an
-ring structure, where an 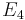 -structure is defined by replacing the operad of infinite-dimensional cubes in infinite-dimensional space by 4-dimensional cubes in 4-dimensional space in the definition of
-structure is defined by replacing the operad of infinite-dimensional cubes in infinite-dimensional space by 4-dimensional cubes in 4-dimensional space in the definition of 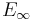 -ring spectra. It can be shown that if Brown–Peterson cohomology has an
-ring spectra. It can be shown that if Brown–Peterson cohomology has an 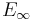 structure, it is not compatible with the usual map
structure, it is not compatible with the usual map 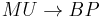 from complex cobordism (see Johnson, Noel 2010).
from complex cobordism (see Johnson, Noel 2010).
Constructions
One of the main advantage of highly structured ring spectra is that they allow many constructions.
- They form a model category and therefore one can take (homotopy) limits and colimits.
- Modules over a highly structured ring spectrum form a stable model category. In particular, their homotopy category is triangulated. If the ring spectrum has an
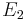 -structure, the category of modules has a monoidal (smash) product; if it is at least
-structure, the category of modules has a monoidal (smash) product; if it is at least 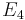 , then it has a symmetric monoidal (smash) product.
, then it has a symmetric monoidal (smash) product. - One can form group ring spectra.
- One can define the algebraic K-theory/topological Hochschild homology/... of a highly structured ring spectrum
- One can define the space of units, which is crucial for certain questions of orientability (of bundles).
References
- A. Baker and A. Jeanneret: Brave new Hopf algebroids and extensions of MU-algebras, Homology, Homotopy and Applications 4 (2002) 163-173.
- A.D. Elmendorf, I. Kriz, M.A. Mandell, and J. P.May, Rings, modules, and algebras in stable homotopy theory, AMS (2007), ISBN 0821843036
- N. Johnson, J. Noel, For complex orientations preserving power operations, p-typicality is atypical, Topology and its Applications 157, issue 14, p. 2271-2288 (2010)
- J. Lurie, Higher Algebra
- M. A. Mandell, J. P. May, S. Schwede and B. Shipley, Model Categories of Diagram Spectra, Proc. London Math. Soc. (3) 82, 441-512 (2001).
- M. Basterra, M. A. Mandell, The multiplication on BP (2010)
- J. Peter May,
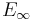 -ring spaces and
-ring spaces and 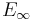 -ring spectra, Springer (1977), http://www.math.uchicago.edu/~may/BOOKSMaster.html
-ring spectra, Springer (1977), http://www.math.uchicago.edu/~may/BOOKSMaster.html - J. Peter May, What precisely are
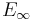 ring spaces and
ring spaces and 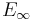 ring spectra? (2009)
ring spectra? (2009) - S. Schwede, S-modules and symmetric spectra, Math. Ann. 319, 517–532 (2001)
- S. Schwede, An untitled book project about symmetric spectra (2007)